Trends with the GOZCARDS DatasetΒΆ
Here we calculate trends using the GOZCARDS dataset by regressing to the VMR monthly zonal means using seasonal terms in our predictors.
[2]:
import xarray as xr
import numpy as np
from LOTUS_regression.regression import regress_all_bins
from LOTUS_regression.predictors.seasonal import add_seasonal_components
from LOTUS_regression.predictors import load_data
The GOZCARDS data is in multiple NetCDF4 files. Load them all in and concatenate on the time dimension. Also only take values in the latitude range -60 to 60.
[3]:
GOZCARDS_FILES = r'/media/users/data/LOTUS/GOZCARDS/*.nc4'
data = xr.decode_cf(xr.open_mfdataset(GOZCARDS_FILES, concat_dim='time', group='Merged', engine='netcdf4'))
data = data.loc[dict(lat=slice(-60, 60))]
print(data)
<xarray.Dataset>
Dimensions: (data_source: 6, lat: 12, lev: 25, overlap: 6, time: 384)
Coordinates:
* lat (lat) float32 -55.0 -45.0 -35.0 ... 35.0 45.0 55.0
* lev (lev) float32 1e+03 681.3 464.2 ... 0.2154 0.1468 0.1
* time (time) datetime64[ns] 1979-01-15 ... 2012-12-15
* data_source (data_source) int32 1 2 3 4 5 6
* overlap (overlap) int32 1 2 3 4 5 6
Data variables: (12/13)
data_source_name (time, data_source) |S20 dask.array<chunksize=(12, 6), meta=np.ndarray>
overlap_start_time (time, overlap) datetime64[ns] dask.array<chunksize=(12, 6), meta=np.ndarray>
overlap_end_time (time, overlap) datetime64[ns] dask.array<chunksize=(12, 6), meta=np.ndarray>
overlap_used_source (time, overlap, data_source) int8 dask.array<chunksize=(12, 6, 6), meta=np.ndarray>
overlap_source_total (time, overlap, data_source, lev, lat) float64 dask.array<chunksize=(12, 6, 6, 25, 12), meta=np.ndarray>
average (time, lev, lat) float32 dask.array<chunksize=(12, 25, 12), meta=np.ndarray>
... ...
std_dev (time, lev, lat) float32 dask.array<chunksize=(12, 25, 12), meta=np.ndarray>
std_error (time, lev, lat) float32 dask.array<chunksize=(12, 25, 12), meta=np.ndarray>
minimum (time, lev, lat) float32 dask.array<chunksize=(12, 25, 12), meta=np.ndarray>
maximum (time, lev, lat) float32 dask.array<chunksize=(12, 25, 12), meta=np.ndarray>
offset (time, data_source, lev, lat) float32 dask.array<chunksize=(12, 6, 25, 12), meta=np.ndarray>
offset_std_error (time, data_source, lev, lat) float32 dask.array<chunksize=(12, 6, 25, 12), meta=np.ndarray>
Attributes:
OriginalFileVersion: 1.01
OriginalFileProcessingCenter: Jet Propulsion Laboratory / California Ins...
InputOriginalFile: All available original source data for the...
DataQuality: All data screening according to the specif...
DataSource: SAGE-I v5.9_rev, SAGE-II v6.2, HALOE v19, ...
DataSubset: Full Dataset
Load some standard predictors and add a constant
[4]:
predictors = load_data('pred_baseline_pwlt.csv')
print(predictors.columns)
Index(['enso', 'solar', 'qboA', 'qboB', 'aod', 'linear_pre', 'linear_post',
'constant'],
dtype='object')
Currently our predictors have no seasonal dependence. Add in some seasonal terms with different numbers of Fourier components.
[5]:
predictors = add_seasonal_components(predictors, {'constant': 4, 'linear_pre': 2, 'linear_post': 2, 'qboA': 2, 'qboB': 2})
print(predictors[:5])
enso solar qboA qboB aod linear_pre \
time
1979-01-01 0.499274 1.568564 -0.991782 -0.925437 -0.395539 -1.800000
1979-02-01 0.281624 1.622217 -1.024426 -1.028774 -0.396092 -1.791667
1979-03-01 -0.070762 1.312212 -1.147750 -0.659631 -0.397189 -1.783333
1979-04-01 0.219438 1.127112 -1.138165 -0.399319 -0.399997 -1.775000
1979-05-01 0.291988 1.002103 -1.205567 0.058949 -0.403881 -1.766667
linear_post constant qboA_sin0 qboA_cos0 ... \
time ...
1979-01-01 0.0 1.0 -0.000000 -0.991782 ...
1979-02-01 0.0 1.0 -0.520774 -0.882181 ...
1979-03-01 0.0 1.0 -0.974957 -0.605631 ...
1979-04-01 0.0 1.0 -1.137875 -0.025696 ...
1979-05-01 0.0 1.0 -1.061723 0.571085 ...
linear_post_sin1 linear_post_cos1 constant_sin0 constant_cos0 \
time
1979-01-01 0.0 0.0 0.000000 1.000000
1979-02-01 0.0 0.0 0.508356 0.861147
1979-03-01 0.0 -0.0 0.849450 0.527668
1979-04-01 0.0 -0.0 0.999745 0.022576
1979-05-01 -0.0 -0.0 0.880683 -0.473706
constant_sin1 constant_cos1 constant_sin2 constant_cos2 \
time
1979-01-01 0.000000 1.000000 0.000000 1.000000
1979-02-01 0.875539 0.483147 0.999579 -0.029025
1979-03-01 0.896456 -0.443132 0.096613 -0.995322
1979-04-01 0.045141 -0.998981 -0.997707 -0.067683
1979-05-01 -0.834370 -0.551205 -0.090190 0.995925
constant_sin3 constant_cos3
time
1979-01-01 0.000000 1.000000
1979-02-01 0.846029 -0.533137
1979-03-01 -0.794497 -0.607268
1979-04-01 -0.090190 0.995925
1979-05-01 0.919817 -0.392347
[5 rows x 32 columns]
Perform the regression and convert the coefficients to percent anomaly.
[6]:
results = regress_all_bins(predictors, data['average'], tolerance=0.1)
# Convert to ~ percent
results /= data['average'].mean(dim='time')
results *= 100
print(results)
<xarray.Dataset>
Dimensions: (lat: 12, lev: 25)
Coordinates:
* lev (lev) float32 1e+03 681.3 464.2 ... 0.2154 0.1468 0.1
* lat (lat) float32 -55.0 -45.0 -35.0 ... 35.0 45.0 55.0
Data variables: (12/64)
enso (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
enso_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
solar (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
solar_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
qboA (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
qboA_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
... ...
constant_cos2 (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
constant_cos2_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
constant_sin3 (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
constant_sin3_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
constant_cos3 (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
constant_cos3_std (lev, lat) float64 dask.array<chunksize=(25, 12), meta=np.ndarray>
[7]:
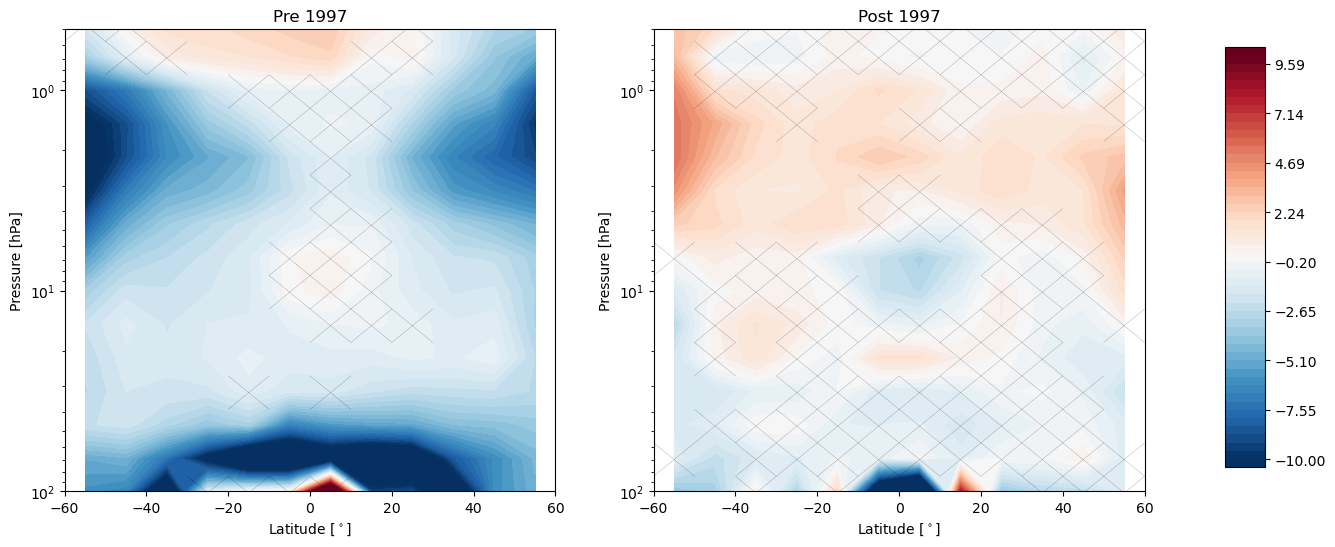
import LOTUS_regression.plotting.trends as trends
trends.pre_post_with_confidence(results, x='lat', y='lev', ylim=(100, 0.5), log_y=True, figsize=(16, 6),
x_label='Latitude [$^\circ$]', y_label='Pressure [hPa]', pre_title='Pre 1997',
post_title='Post 1997')
